How to Write Complex Formulas in Survey123: Empower Your Users

Quick Summary

• Survey123's XLSForm expression language uses div instead of / for division and int() instead of floor(), which requires care when writing multi-step calculation formulas.
• Dymaptic used Survey123 complex formulas to convert pipe defect measurements (distance and diameter) into degrees and clock-face positions for field inspections.
• The calculation type in Survey123 hides intermediate values to keep forms clean, and the decimal type is useful for step-by-step debugging.
• This post includes the full Survey123 expression language formulas and a worked example using real pipeline inspection data.

How Do Complex Formulas Work in Survey123?

Survey123 is an invaluable tool for data collection within the ArcGIS ecosystem. Survey123 covers use cases from collecting simple data via online forms to supporting complex inspections in a disconnected environment. This post walks through a real dymaptic client project to show how it's done.

Recently we helped out a client at dymaptic with some complex formulas in Survey123, and I thought it would be a wonderful excuse to talk about the power of calculations in Survey123. This post contains some math and assumes that you already know how to edit a form using Excel and Survey123 Connect with the XLSForm specification that Survey123 uses. You can find more in the documentation.

A few tips before getting started:

• I'm using the decimal type for demonstration here, but you can use calculation instead to hide the intermediate values
• The Survey123 calculation language is a little hard to read; I suggest making multiple steps using the calculation type
• If you want to keep the intermediate steps, keep the decimal type and hide those fields

What Makes the Survey123 Expression Language Different from Standard Math Notation?

The language used in Survey123 (or the XLSForm specification that Survey123 uses) can be a little bit tough. The thing that gets most people right off the bat is the division operator. You can't use /; you have to use div. I know, strange. That's the strangest one though.

It does include things like pi() for pi and some basic math functions. The part we need for this tutorial though is a floor function that doesn't exist. Fortunately, the int function does effectively the same thing. It will always round down, so int(9.1) = int(9.9) = 9.

For the complete listing of math operators that can be used when creating complex formulas in Survey123, as well as some other useful ones like regular expressions, see the XLSForm documentation.

How Do You Convert Distance Measurements to Degrees in Survey123?

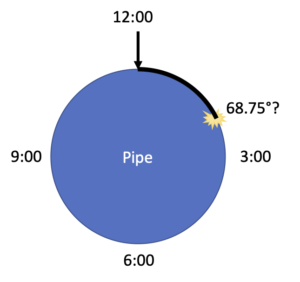
In our scenario, users were inspecting a buried pipeline (Survey123 is great for inspecting all kinds of assets, even things like buried water lines) and noting the position of a defect or problem on the line by measuring it using a tape measure from the top of the pipe:

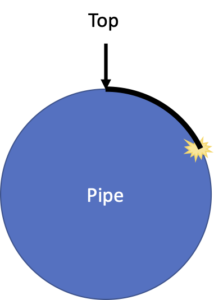
If you imagine that we cut the pipe in half and look at the open end of it, that's the cross-section. In the image, you can see the location we want to measure and how we would measure its position from the top of the pipe.

So now we know two things:

• The distance to our defect (3 inches)
• The diameter of our pipe (5 inches) (our database already knows this because our GIS is robust)

Computers prefer to see things like this in degrees where 0 is the top of the pipe, 90 is to the right, 180 at the bottom, and 270 to the left:

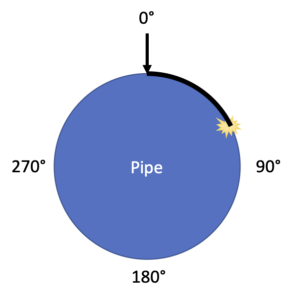
We can solve this with a simple proportion:

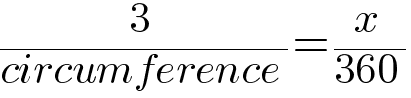
But how do we get the circumference? Fortunately, Archimedes¹ has us covered with the formula C = pi * d. And we have d, it's our diameter, so that gives us:

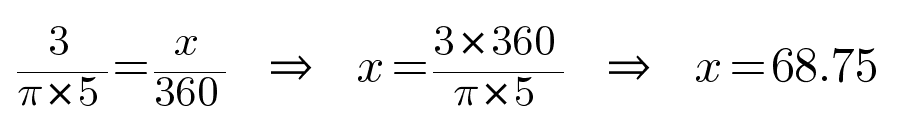
So, x is 68.75 degrees. Doing a quick check, that looks right; it's about 75% of the way around to our 90-degree mark.

Now we can write that using the Survey123 expression language like this:

360 * ${distance} div (pi() * ${diameter})

How Do You Convert Degrees to a Clock Position in Survey123?

Degrees are great for computers, but they are kind of hard for humans to understand. Fortunately, that cross-section looks like something we are all familiar with: a clock. We need to calculate the hours and the minutes. Hours look like another ratio problem...

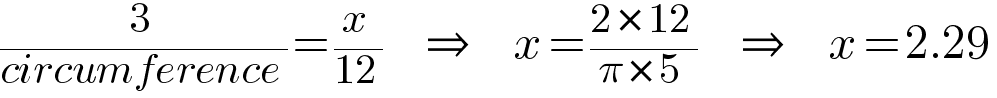
So, x is 2.29, a little after 2:00 on our pipe. Looks good. We can translate that into Survey123 expression language like this:

12 * ${distance} div (pi() * ${diameter})

But how do we get the minutes? Well, we know there are 60 minutes in an hour so: 0.29 * 60 = 17.4, which gives us 2:17.

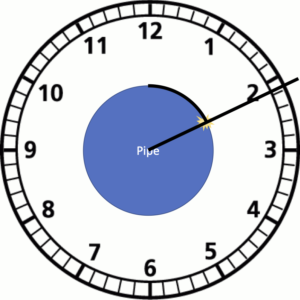
Remember: we are only looking at the hour hand here, so it's the hour hand at 2:00 + 17 minutes. To get this in Survey123 we can simply subtract the floor() of the number:

2.29 - floor(2.29) = 2.29 - 2 = 0.29
Hours = floor((3*12) / (pi*5))
Minutes = ((3*12) / (pi*5) - Hours) * 60

Unfortunately, there is no floor() function in the Survey123 expression language. But we do have int(). It turns out that int behaves the same way as floor (see notes above), so we can build our complex Survey123 formulas like this:

decimal_hours = 12 * ${distance} div (pi() * ${diameter})
floor_hours = int(${decimal_hours})
decimal_minutes = (${decimal_hours} - ${floor_hours}) * 60
clock_position = string(${floor_hours}) + ":" + string(round(${decimal_minutes}, 0))

I snuck in one final round() to trim the decimal places off of the minutes here, which causes it to round to 18 minutes instead of 17.

¹ Archimedes didn't understand pi yet, but he did figure out the relationship between circumference and diameter by calculating the perimeters of inscribed regular polygons.

Clock picture from clipartbest.com. XLSForm formula images built with math.tools. All other art is the author's own.